Bevan point

In geometry, the Bevan point, named after Benjamin Bevan, is a triangle center. It is defined as center of the Bevan circle, that is the circle through the centers of the three excircles of a triangle.

Reference triangle

△ ABC

Excentral triangle

△ M A M B M C

of

△ ABC

Circumcircle of

△ M A M B M C

(Bevan circle of

△ ABC

, centered at Bevan point

M

)

Reference triangle

△ ABC

Excentral triangle

△ M A M B M C

of

△ ABC

Bevan circle

k M

of

△ ABC

(centered at Bevan point

M

)

Euler line

e

, on which circumcenter

O

, orthocenter

H

, centroid

G

, and de Longchamps point

L

lie

Other points: incenter

I

, Nagel point

N

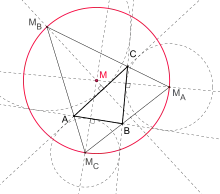
The Bevan point of a triangle is the reflection of the incenter across the circumcenter of the triangle.

The Bevan point $M$ of triangle $△ ABC$ has the same distance from its Euler line $e$ as its incenter $I$ and the circumcenter $O$ is the midpoint of the line segment $MI$ . The length of $MI$ is given by

{\overline {MI}}=2{\sqrt {R^{2}-{\frac {abc}{a+b+c}}}}

where $R$ denotes the radius of the circumcircle and $a, b, c$ the sides of $△ ABC$ . The Bevan is point is also the midpoint of the line segment $NL$ connecting the Nagel point $N$ and the de Longchamps point $L$ . The radius of the Bevan circle is $2 R$ , that is twice the radius of the circumcircle.

External links

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.