Ancient Egyptian units of measurement
The ancient Egyptian units of measurement are those used by the dynasties of ancient Egypt prior to its incorporation in the Roman Empire and general adoption of Roman, Greek, and Byzantine units of measurement. The units of length seem to have originally been anthropic, based on various parts of the human body, although these were standardized using cubit rods, strands of rope, and official measures maintained at some temples.
Following Alexander the Great's conquest of Persia and subsequent death, his bodyguard and successor Ptolemy assumed control in Egypt, partially reforming its measurements, introducing some new units and hellenized names for others.
Length
Egyptian units of length are attested from the Early Dynastic Period. Although it dates to the 5th dynasty, the Palermo stone recorded the level of the Nile River during the reign of the Early Dynastic pharaoh Djer, when the height of the Nile was recorded as 6 cubits and 1 palm[1] (about 3.217 m or 10 ft 6.7 in). A Third Dynasty diagram shows how to construct an elliptical vault using simple measures along an arc. The ostracon depicting this diagram was found near the Step Pyramid of Saqqara. A curve is divided into five sections and the height of the curve is given in cubits, palms, and digits in each of the sections.[2] [3]
At some point, lengths were standardized by cubit rods. Examples have been found in the tombs of officials, noting lengths up to remen. Royal cubits were used for land measures such as roads and fields. Fourteen rods, including one double-cubit rod, were described and compared by Lepsius.[4] Two examples are known from the Saqqara tomb of Maya, the treasurer of Tutankhamun. Another was found in the tomb of Kha (TT8) in Thebes. These cubits are about 52.5 cm (20.7 in) long and are divided into palms and hands: each palm is divided into four fingers from left to right and the fingers are further subdivided into ro from right to left. The rules are also divided into hands[5] so that for example one foot is given as three hands and fifteen fingers and also as four palms and sixteen fingers.[6][3][7][8][9][5]

Surveying and itinerant measurement were undertaken using rods, poles, and knotted cords of rope. A scene in the tomb of Menna in Thebes shows surveyors measuring a plot of land using rope with knots tied at regular intervals. Similar scenes can be found in the tombs of Amenhotep-Sesi, Khaemhat and Djeserkareseneb. The balls of rope are also shown in New Kingdom statues of officials such as Senenmut, Amenemhet-Surer, and Penanhor.[2]
| Names | Equivalents | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| English | Egyptian | Coptic | Palms | Digits | Metric[10] | ||||||||
| Digit[11] Finger[12] Fingerbreadth[11] Tebā[13] |
ḏbꜥ | ⲧⲏⲏⲃⲉ[15][16] | tēēbe | 1⁄4 | 1 | 1.875 cm | |||||||
| Palm[11] Hand[17] Shesep[18] |
šsp | ϣⲟⲡ[19][16] ϣⲟⲟⲡ[19] ϣⲱⲡ[19] ϣⲁⲡ[19] | shop shoop shōp shap |
1 | 4 | 7.5 cm | |||||||
| Hand[20] Handsbreadth[18] |
ḏrt | ϩⲱϩϥ[21][22] | hōhf | 1+1⁄4 | 5 | 9.38 cm | |||||||
| Fist[18] | ḫfꜥ[18] ꜣmm[14] | ϭⲁϫⲙⲏ[23] ϫⲁⲙⲏ[23] | qajmē jamē |
1+1⁄2 | 6 | 11.25 cm | |||||||
| Double Handbreadth[14] | šspwy | 2 | 8 | 15 cm[14] | |||||||||
| Small Span[18] Pedj-Sheser Shat Nedjes[18] Little Shat[12] |
pḏ šsr šꜣt nḏs[18] |
ⲣⲧⲱ[24][22] ⲉⲣⲧⲱ[25] |
rtō ertō |
3 | 12 | 22.5 cm | |||||||
| Great Span[18] Half-Cubit[14] Pedj-Aa Shat Aa[18] Great Shat[12] |
pḏ ꜥꜣ[18][14] šꜣt ꜥꜣ[18] |
3+1⁄2 | 14 | 26 cm | |||||||||
| Foot Djeser[18] Ser[13] Bent Arm[18] |
ḏsr | 4 | 16 | 30 cm | |||||||||
| Shoulder Remen[18] Upper Arm[18] |
rmn | 5 | 20 | 37.5 cm | |||||||||
| Small Cubit[20] Short Cubit[18] Meh Nedjes[18] |
mḥ nḏs mḥ šsr |
ⲙⲁϩⲉ[26][16] ⲙⲉϩⲓ[27] |
mahe mehi |
6 | 24 | 45 cm | |||||||
| Cubit Royal Cubit[18] Sacred Cubit[17] Meh Nesut[11] Meh Nisut[18] Mahi Ell[26] |
mḥ | 7 | 28 | 52.3 cm[11] 52.5 cm[17] | |||||||||
| Pole Nebiu[28] |
nbiw | 8 | 32 | 60 cm | |||||||||
| Rod Rod of Cord Stick of Rope[20] Khet[11] Schoinion[29] |
ḫt | ϩⲱⲧⲉ[31] ϩⲱϯ[31] | hōte hōti |
100 cubits[11] | 52.5 m[29] | ||||||||
| Schoenus[14] River-Measure League[14] Ater[11] Iter[20] or Iteru[14] |
i͗trw | ϣϥⲱ[32] ϣⲃⲱ[32] | shfō shvō |
20,000 cubits[11] | 10.5 km[11] | ||||||||
The digit was also subdivided into smaller fractions of 1⁄2, 1⁄3, 1⁄4, and 1⁄16.[33] Minor units include the Middle Kingdom reed of 2 royal cubits,[lower-alpha 10] the Ptolemaic xylon (Greek: ξύλον, lit. "timber") of three royal cubits,[34][35] the Ptolemaic fathom (Greek: ὀργυιά, orgyiá; Ancient Egyptian: ḥpt; Coptic: ϩⲡⲟⲧ, hpot) of four lesser cubits,[36] and the kalamos of six royal cubits.[17]
Area
Records of land area also date to the Early Dynastic Period. The Palermo stone records grants of land expressed in terms of kha and setat. Mathematical papyri also include units of land area in their problems. For example, several problems in the Moscow Mathematical Papyrus give the area of rectangular plots of land in terms of setat and the ratio of the sides and then require the scribe to solve for their exact lengths.[6]
The setat was the basic unit of land measure and may originally have varied in size across Egypt's nomes.[20] Later, it was equal to one square khet, where a khet measured 100 cubits. The setat could be divided into strips one khet long and ten cubit wide (a kha).[2][6][37]
During the Old Kingdom:
| Names | Equivalents[38] | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| English | Egyptian | Coptic | Setat | Square Cubits |
Metric | |||||||
| Sa[20] Eighth |
zꜣ | 1⁄800 | 12+1⁄2 | 3.4456 m2 | ||||||||
| Heseb Fourth Account Unit[20] |
ḥsb | 1⁄400 | 25 | 6.8913 m2 | ||||||||
| Remen Half Shoulder[20] |
rmn | 1⁄200 | 50 | 13.783 m2 | ||||||||
| Ta Khet[38] Cubit[39] Cubit of Land[39] Land Cubit[14] Ground Cubit[39] Cubit Strip[39] Land Unit[20] |
tꜣ ḫt mḥ mḥ itn |
ϫⲓⲥⲉ[40][22] | jise | 1⁄100 | 100[38] | 27.565 m2 | ||||||
| Kha Thousand[20] |
ḫꜣ | 1⁄10 | 1,000 | 275.65 m2 | ||||||||
| Setat[38] Setjat[38] Aroura[38] Square Khet[38] |
sṯꜣ[29] sṯꜣt[38] |
ⲥⲱⲧ[41][22] ⲥⲧⲉⲓⲱϩⲉ[42][22] | sōt steiōhe |
1 | 10,000 | 2,756.5 m2 | ||||||
During the Middle and New Kingdom, the "eighth", "fourth", "half", and "thousand" units were taken to refer to the setat rather than the cubit strip:
| Sa Eighth |
sꜣ | 1⁄8 | 1,250 | 345 m2 | |||||
| Heseb Fourth |
hsb r-fdw | 1⁄4 | 2,500 | 689 m2 | |||||
| Gs Remen Half |
gs | ⲣⲉⲣⲙⲏ[22] | rermē | 1⁄2 | 5,000 | 1378 m2 | |||
| Kha Thousand |
ḫꜣ ḫꜣ tꜣ | 10 | 100,000 | 2.76 ha | |||||
During the Ptolemaic period, the cubit strip square was surveyed using a length of 96 cubits rather than 100, although the aroura was still figured to compose 2,756.25 m2.[17] A 36 square cubit area was known as a kalamos and a 144 square cubit area as a hamma.[17] The uncommon bikos may have been 1+1⁄2 hammata or another name for the cubit strip.[17] The Coptic shipa (ϣⲓⲡⲁ) was a land unit of uncertain value, possibly derived from Nubia.[43]
Volume

Units of volume appear in the mathematical papyri. For example, computing the volume of a circular granary in RMP 42 involves cubic cubits, khar, heqats, and quadruple heqats.[6][9] RMP 80 divides heqats of grain into smaller henu.

| Names | Equivalents | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| English | Egyptian | Heqats | Ro | Metric | ||||||||
| Ro | r | 1⁄320 | 1 | 0.015 L | ||||||||
| Dja | dja | 1⁄16 | 20[44] | 0.30 L | ||||||||
| Jar Hinu |
hnw | 1⁄10 | 32 | 0.48 L | ||||||||
| Barrel Heqat Hekat |
hqt | 1 | 320 | 4.8 L | ||||||||
| Double Barrel Double Heqat Double Hekat |
hqty | 2 | 640 | 9.6 L | ||||||||
| Quadruple Heqat (MK)[45] Oipe[46] (NK)[45] |
hqt-fdw jpt[20] ipt[45] |
4 | 1,280 | 19.2 L | ||||||||
| Sack Khar |
khar | 20 (MK) 16 (NK)[47] |
6,400 (MK) 5120 (NK) |
96.5 L (MK) 76.8 L (NK)[47] | ||||||||
| Deny Cubic cubit |
deny | 30 | 9,600 | 144 L | ||||||||
The oipe was also formerly romanized as the apet.[48]
Weight


Weights were measured in terms of deben. This unit would have been equivalent to 13.6 grams in the Old Kingdom and Middle Kingdom. During the New Kingdom however it was equivalent to 91 grams. For smaller amounts the qedet (1⁄10 of a deben) and the shematy (1⁄12 of a deben) were used.[2][9]
| Names | Equivalents | |||||||
|---|---|---|---|---|---|---|---|---|
| English | Egyptian | Debens | Metric | |||||
| Piece Shematy |
shȝts | 1⁄12 | ||||||
| Qedet Kedet Kite |
qdt | 1⁄10 | ||||||
| Deben | dbn | 1 | 13.6 g (OK & MK) 91 g (NK) | |||||
The qedet or kedet is also often known as the kite, from the Coptic form of the same name (ⲕⲓⲧⲉ or ⲕⲓϯ).[49] In 19th-century sources, the deben and qedet are often mistakenly transliterated as the uten and kat respectively, although this was corrected by the 20th century.[50]
Time
The former annual flooding of the Nile organized prehistoric and ancient Egypt into three seasons: Akhet ("Flood"), Peret ("Growth"), and Shemu or Shomu ("Low Water" or "Harvest").[51][52][53]
The Egyptian civil calendar in place by Dynasty V[54] followed regnal eras resetting with the ascension of each new pharaoh.[55] It was based on the solar year and apparently initiated during a heliacal rising of Sirius following a recognition of its rough correlation with the onset of the Nile flood.[56] It followed none of these consistently, however. Its year was divided into 3 seasons, 12 months, 36 decans, or 360 days with another 5 epagomenal days[57]—celebrated as the birthdays of five major gods[58] but feared for their ill luck[59]—added "upon the year". The Egyptian months were originally simply numbered within each season[60] but, in later sources, they acquired names from the year's major festivals[61] and the three decans of each one were distinguished as "first", "middle", and "last".[62] It has been suggested that during the Nineteenth Dynasty and the Twentieth Dynasty the last two days of each decan were usually treated as a kind of weekend for the royal craftsmen, with royal artisans free from work.[63] This scheme lacked any provision for leap year intercalation until the introduction of the Alexandrian calendar by Augustus in the 20s BC, causing it to slowly move through the Sothic cycle against the solar, Sothic, and Julian years.[6][3][64] Dates were typically given in a YMD format.[55]
The civil calendar was apparently preceded by an observational lunar calendar which was eventually made lunisolar[lower-alpha 17] and fixed to the civil calendar, probably in 357 BC.[67] The months of these calendars were known as "temple months"[68] and used for liturgical purposes until the closing of Egypt's pagan temples under Theodosius I[69] in the AD 390s and the subsequent suppression of individual worship by his successors.[70]
Smaller units of time were vague approximations for most of Egyptian history. Hours—known by a variant of the word for "stars"[71]—were initially only demarcated at night and varied in length. They were measured using decan stars and by water clocks. Equal 24-part divisions of the day were only introduced in 127 BC. Division of these hours into 60 equal minutes is attested in Ptolemy's 2nd-century works.
| Name | Days | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| English | Egyptian | |||||||||
| hour | wnwt | variable | ||||||||
| day | sw | 1 | ||||||||
| decan decade week | "ten-day" sw mḏ[81] |
10 | ||||||||
| month | ꜣbd | 30 | ||||||||
| season | ı͗trw[lower-alpha 22] | 120 | ||||||||
| year | rnpt | 365 365+1⁄4 | ||||||||
See also
Notes
- Alternative representations for the Egyptian digit include
and

.[14]



- Alternative representations for the Egyptian palm include
,
,
and
.[14]


- Alternative representations for the Egyptian hand include
,

, and


.[14]


- Alternative representations for the Egyptian fist include
and



as ḫfꜥ and




,



, and




as ꜣmm.[14]


- Alternative representations for the Egyptian double handbreadth include
.[14]

- Alternative representations for the Egyptian half-cubit include
of uncertain pronunciation.[14]Z12 - Alternative representations of the Egyptian cubit or royal cubit include
,
,

,

,

,

,[14] all pronounced mḥ,[14] and the explicit "royal" or "sacred cubit"


,[13] pronounced mḥ nswt[14] or ni͗-swt.[18]
![X1 [t] t](../I/hiero_X1.png.webp)
![N35 [n] n](../I/hiero_N35.png.webp)

- Alternative representations of the Egyptian rod include
[30] and
,






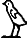
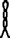
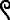
, and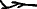






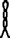
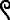
,[14] which were pronounced ḫt n nwḥ[11] (Coptic: ϣⲉ ⲛ ⲛⲟϩ, she n noh).[22]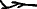





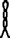
- Alternative representations of the Egyptian schoenus include
,


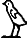
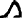
,


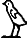
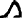

,


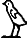

,



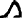


,




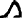
,








,








,






, and





.[14]

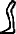
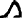
- The Egyptian reed was written
or


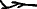
and pronounced nbi͗.[14]



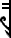
- Alternative representations of the 100-square-cubit measure include
and
, both pronounced mḥ tꜣ,[14] and

.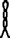




- Alternative representations of the setat include
,
,

,


,

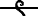


,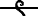


,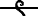




,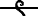



,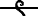

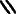
, and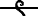

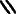



, all pronounced sṯꜣt.[14]



- Alternative representations of the 1⁄8 setat include
.[14]Z30 - Alternative representations of the quarter-setat include
.

- Alternative representations of the half-setat include
, pronounced gs,


, pronounced rmn,[14] and
.

- Alternative representations of the thousand-ta measure include
,



, and

.[14]





- Parker extensively developed the thesis that the predynastic lunar calendar was already lunisolar, using intercalary months every 2 or 3 years to maintain Sirius's return to the night sky in its twelfth month,[65] but no evidence of such intercalation exists predating the schematic lunisolar calendar developed in 4th century BC.[66]
- Variant representations of hour include
,[72]

,




,




,[73]






,







,






(properly





with a star at the end of the line and a second shorter line to its right),[71]N46B
,[74]






,[75]

,


,



,


,[76]



,[77]


,[78] and


. As nwt, hour also appears as




.[79]


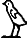


- Variant representations of day include
,[80]
,[81] and


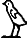

.[82] In the plural sww, it appears as

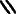

[83]
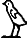


[84] and
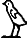


.[81] As hrw ("daytime", "day"), it appears as



,[80]

,[85]

,[86]


,[87]



,[88]




,[89]





,[90]




,[91]
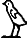


,

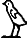

,[92]



,



,



,[93] and



.[94] As rꜥ ("sun", "day"), it appears as

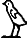


,
,[80] and

.[95] As ḏt, day appears as



, although properly the loaf and stroke are smaller and fit within the curve of the snake.[96]



- Variant representations of decan include
.[82]




- Variant representations of month include
,
,

,[97]


,


,




,




, and





.[98] In the plural ꜣbdtyw, it appears as




.[97] As ꜣbdw, month appears as







.[99]


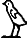
- In the plural ı͗trw, "seasons" appears as
(properly


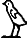

with a triangular leaf),[100]M5B
, and


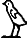
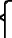
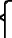
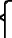



, although properly the palm branches of the last are reversed.[101] As tr ("time", "period", "season"), it appears as






,[102]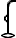

,[103]



,[104] and

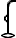

.[105] In the dual number, this appears as trwy in


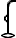

,

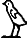
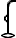


,[104] and

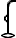


.[105] In the plural, this appears as trw in


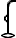
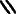
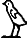


,[106]
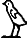


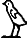
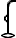


,[103] and


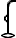


.[104]

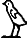
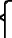


- Variant representations of year include
,
,[102]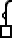


and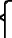

.[107] In the plural rnpwt, it appears as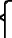



on the Naucratis Stela[108] and as



,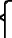
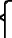
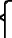
,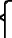
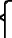
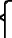




,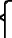
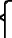


,



,[107] and


.[102]

References
Citations
- Clagett 1999, p. 3.
- Corinna Rossi, Architecture and Mathematics in Ancient Egypt, Cambridge University Press, 2007
- Englebach, Clarke (1990). Ancient Egyptian Construction and Architecture. New York: Dover. ISBN 0486264858.
- Lepsius (1865), pp. 57 ff.
- Loprieno, Antonio (1996). Ancient Egyptian. New York: CUP. ISBN 0521448492.
- Clagett (1999).
- Gardiner, Allen (1994). Egyptian Grammar 3rd Edition. Oxford: Griffith Institute. ISBN 0900416351.
- Faulkner, Raymond (1991). A Concise Dictionary of Middle Egyptian. Griffith Institute Asmolean Museum, Oxford. ISBN 0900416327.
- Gillings, Richard (1972). Mathematics in the Time of the Pharaohs. MIT. ISBN 0262070456.
- Gardiner, §266, pp. 199–200.[3][8][9]
- Clagett (1999), p. 7.
- Clagett (1999), p. 9.
- Lepsius (1865), p. 43.
- Vygus, Mark (2015), Middle Egyptian Dictionary (PDF).
- Crum (1939), p. 597.
- Journal of Egyptian Archaeology, Vol. IV, Egypt Exploration Fund, 1917, p. 135.
- Bagnall (2009), p. 186.
- Clagett (1999), p. 8.
- Crum (1939), p. 574.
- Dollinger, André (2012), "Counting and Measuring", Pharaonic Egypt, Reshafim
{{citation}}: CS1 maint: location missing publisher (link). - Crum (1939), p. 742.
- Feder, Frank; et al., Online Coptic Dictionary, Washington: Georgetown.
- Crum (1939), p. 842.
- Crum (1939), p. 305.
- Crum (1939), p. 58.
- Crum (1939), p. 210.
- Crum (1939), p. 211.
- Obenga, Théophile (2004), African Philosophy: The Pharaonic Period 2780–330 BC, Per Ankh, p. 460.
- Bagnall (2009), p. 185.
- Abd el-Mohsen Bakir (1978), Hat-'a em Sbayet r-en Kemet: An Introduction to the Study of the Egyptian Language: A Semitic Approach, General Egyptian Book Organization, p. 70.
- Crum (1939), p. 722.
- Crum (1939), p. 611.
- Lepsius (1865), p. 44.
- Ridgeway, William (1890), "Mensura", A Dictionary of Greek and Roman Antiquities, London: John Murray.
- Transactions and Proceedings, American Philological Association, 1941, p. 443.
- Janssen, Jozef M.A. (1956), "3997: Iversen, Erik, Canon and Proportions in Egyptian Art", Annual Egyptological Bibliography 1955, Leiden: E.J. Brill for the International Association of Egyptologists, p. 1313.
- Digital Egypt: Measuring area in Ancient Egypt
- Clagett (1999), p. 12.
- Clagett (1999), p. 13.
- Crum (1939), p. 790.
- Crum (1939), p. 360.
- Crum (1939), p. 367.
- Crum (1939), p. 570.
- Pommerening, T. (2003), "Altagyptische Rezepturen Netrologisch Neu Onterpretiert", Berichte zur Wissenschaftgeschichte, No. 26, p. 1–16. (in German)
- "Measuring Volume in Ancient Egypt", Digital Egypt for Universities, London: University College, 2002.
- Allen, James P. (2014), Middle Egyptian: An Introduction to the Language and Culture of Hieroglyphics, 3rd ed., Cambridge: Cambridge University Press, p. 129, ISBN 9781139917094.
- Katz, Victor J.; et al., eds. (2007), The Mathematics of Egypt, Mesopotamia, China, India, and Islam: A Sourcebook, Princeton University Press, p. 17, ISBN 978-0-691-11485-9.
- "Weights and Measures", Encyclopaedia Britannica, 9th ed., vol. XXIV, 1888.
- Weigall (1908), p. ix.
- Weigall (1908), pp. iii & ix.
- Tetley (2014), p. 39.
- Winlock (1940), p. 453.
- Clagett (1995), p. 4–5.
- Clagett (1995), p. 28.
- Clagett (1995), p. 5.
- Parker (1950), p. 23.
- Parker (1950), p. 7.
- Spalinger (1995), p. 33.
- Spalinger (1995), p. 35.
- Parker (1950), pp. 43–5.
- Clagett (1995), p. 14–15.
- Clagett (1995), p. 4.
- Jauhiainen (2009), p. 39.
- Marshall Clagett, Ancient Egyptian Science: Calendars, clocks, and astronomy, 1989
- Parker (1950), pp. 30–2.
- Tetley (2014), p. 153.
- Clagett (1995), p. 26.
- Parker (1950), p. 17.
- Theodosian Code 16.10.12
- Høyrup, p. 13.
- Vygus (2015), p. 409.
- Vygus (2015), p. 399.
- Vygus (2015), p. 408.
- Vygus (2015), p. 410.
- Vygus (2015), p. 1229.
- Vygus (2015), p. 1239.
- Vygus (2015), p. 1240.
- Vygus (2015), p. 1984.
- Vygus (2015), p. 1382.
- Vygus (2015), p. 1228.
- Vygus (2015), p. 1880.
- Vygus (2015), p. 1881.
- Vygus (2015), p. 1611.
- Vygus (2015), p. 1790.
- Vygus (2015), p. 1500.
- Vygus (2015), p. 2467.
- Vygus (2015), p. 1461.
- Vygus (2015), p. 1477.
- Vygus (2015), p. 1478.
- Vygus (2015), p. 1492.
- Vygus (2015), p. 1495.
- Vygus (2015), p. 1513.
- Vygus (2015), p. 1514.
- Vygus (2015), p. 1471.
- Vygus (2015), p. 75.
- Vygus (2015), p. 822.
- Vygus (2015), p. 1233.
- Vygus (2015), p. 1234.
- Vygus (2015), p. 547.
- Vygus (2015), p. 1156.
- Vygus (2015), p. 1168.
- Vygus (2015), p. 958.
- Vygus (2015), p. 1167.
- Vygus (2015), p. 2386.
- Vygus (2015), p. 2387.
- Vygus (2015), p. 1085.
- Vygus (2015), p. 957.
- Vygus (2015), p. 103.
Bibliography
- Bagnall, Roger Shaler (2009), "Practical Help: Chronology, Geography, Measures, Currency, Names, Prosopography, and Technical Vocabulary", The Oxford Handbook of Papyrology, Oxford: Oxford University Press, pp. 179–196, ISBN 9780199843695.
- Clagett, Marshall (1995), Ancient Egyptian Science: A Source Book, Vol. II: Calendars, Clocks, and Astronomy, Memoirs of the APS, No. 214, Philadelphia: American Philosophical Society, ISBN 9780871692146.
- Clagett, Marshall (1999), Ancient Egyptian Science: A Source Book, Vol. III: Ancient Egyptian Mathematics, Memoirs of the APS, Vol. 232, Philadelphia: American Philosophical Society, ISBN 978-0-87169-232-0.
- Crum, Walter Ewing (1939), A Coptic Dictionary, Oxford: Clarendon Press, p. 210.
- Høyrup, Jens, "A Historian's History of Ancient Egyptian Science" (PDF), Physis, a review of Clagett's Ancient Egyptian Science, Vols. I & II.
- Jauhiainen, Heidi (2009), Do Not Celebrate Your Feast without Your Neighbors: A Study of References to Feasts and Festivals in Non-Literary Documents from Ramesside Period Deir el-Medina (PDF), Publications of the Institute for Asian and African Studies, No. 10, Helsinki: University of Helsinki.
- Lepsius, Karl Richard (1865), Die Alt-Aegyptische Elle und Ihre Eintheilung, Berlin: Dümmler. (in German)
- Parker, Richard Anthony (1950), The Calendars of Ancient Egypt (PDF), Studies in Ancient Oriental Civilization, No. 26, Chicago: University of Chicago Press.
- Spalinger, Anthony (January 1995), "Some Remarks on the Epagomenal Days in Ancient Egypt", Journal of Near Eastern Studies, Vol. 54, No. 1, pp. 33–47.
- Tetley, M. Christine (2014), The Reconstructed Chronology of the Egyptian Kings, Vol. I, archived from the original on 2017-02-11, retrieved 2017-02-24.
- Weigall, Arthur Edward Pearse Brome (1908), Weights and Balances (PDF), Catalogue Général des Antiquités Égyptiennes du Musée du Caire, No. 31271-31670, Cairo: Imprimerie de l'Institut Français d'Archéologie Orientale.
- Winlock, Herbert Eustis (1940), "The Origin of the Ancient Egyptian Calendar", Proceedings of the American Philosophical Society, No. 83, New York: Metropolitan Museum of Art, pp. 447–464.
External links
- Egyptian ceremonial ruler showing fingers, palms, hands, fists, feet, remen
- Cubit divided into fingers and hands
- Modern replica of Egyptian ruler
- Measuring length in Ancient Egypt Page by Digitalegypt (University College London).
- Irrational numbers and pyramids Archived 2015-09-24 at the Wayback Machine Article by Gay Robins and C.C.D. Shute
- Introduction to Egyptian Mathematics, with photographs of Maya's cubit rod from the Louvre and land surveying scenes from the tomb of Menna.