Albers projection
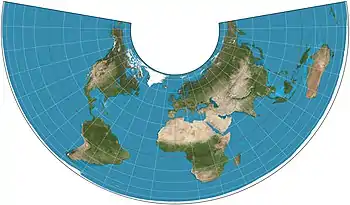
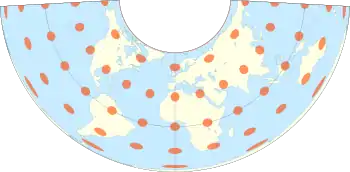
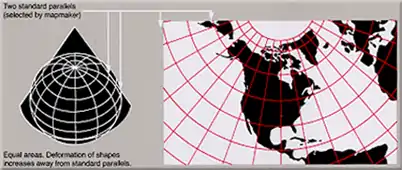
The Albers equal-area conic projection, or Albers projection (named after Heinrich C. Albers), is a conic, equal area map projection that uses two standard parallels. Although scale and shape are not preserved, distortion is minimal between the standard parallels.
Official adoption
The Albers projection is used by some big countries as "official standard projection" for Census and other applications.
| Country | Agency |
|---|---|
| Brazil | federal government, through IBGE, for Census Statistical Grid [1] |
| Canada | government of British Columbia[2] |
| Canada | government of the Yukon[3] (sole governmental projection) |
| USA | United States Geological Survey[4] |
| USA | United States Census Bureau[4] |
Some "official products" also adopted Albers projection, for example most of the maps in the National Atlas of the United States.[5]
Formulas
For Sphere
Snyder[5] describes generating formulae for the projection, as well as the projection's characteristics. Coordinates from a spherical datum can be transformed into Albers equal-area conic projection coordinates with the following formulas, where is the radius, is the longitude, the reference longitude, the latitude, the reference latitude and and the standard parallels:
where
Lambert equal-area conic
If just one of the two standard parallels of the Albers projection is placed on a pole, the result is the Lambert equal-area conic projection.[6]
See also
References
- "Grade Estatística" (PDF). 2016. Archived from the original (PDF) on 2018-02-19.
- "Data Catalogue".
- "Support & Info: Common Questions". Geomatics Yukon. Government of Yukon. Retrieved 15 October 2014.
- "Projection Reference". Bill Rankin. Archived from the original on 25 April 2009. Retrieved 2009-03-31.
- Snyder, John P. (1987). "Chapter 14: ALBERS EQUAL-AREA CONIC PROJECTION". Map Projections – A Working Manual. U.S. Geological Survey Professional Paper 1395. Washington, D.C.: United States Government Printing Office. p. 100. Archived from the original on 2008-05-16. Retrieved 2017-08-28.
- "Directory of Map Projections". "Lambert equal-area conic".
External links
- Mathworld's page on the Albers projection
- Table of examples and properties of all common projections, from radicalcartography.net
- An interactive Java Applet to study the metric deformations of the Albers Projection.