Find Poles of f(z)

The poles of ${\displaystyle f(z)={\frac {1}{z^{n}+1}}\!\,}$ are just the zeros of ${\displaystyle z^{n}+1\!\,}$, so we can compute them in the following manner:

If ${\displaystyle z=re^{i\theta }\!\,}$ is a solution of ${\displaystyle z^{n}+1=0\!\,}$,

then ${\displaystyle z^{n}=r^{n}e^{i\theta n}=-1\!\,}$

${\displaystyle \Rightarrow r=1\!\,}$ and ${\displaystyle in\theta =i(\pi +2\pi k)\!\,}$

${\displaystyle \Rightarrow \theta ={\frac {\pi +2\pi k}{n}}\!\,}$ , k=0,1,2,...,n-1.

Thus, the poles of ${\displaystyle f(z)\!\,}$ are of the form ${\displaystyle z=e^{\frac {\pi +2\pi k}{n}}\!\,}$ with ${\displaystyle k=0,1,...,n-1\!\,}$

Choose Path of Contour Integral

In order to get obtain the integral of ${\displaystyle f(x)\!\,}$ from 0 to ${\displaystyle \infty \!\,}$ , let us consider the path ${\displaystyle \gamma \!\,}$ consisting in a line ${\displaystyle A\!\,}$ going from 0 to ${\displaystyle R\!\,}$, then the arc ${\displaystyle B\!\,}$ of radius ${\displaystyle R\!\,}$ from the angle 0 to ${\displaystyle {\frac {2\pi }{n}}\!\,}$ and then the line ${\displaystyle C\!\,}$ joining the end point of ${\displaystyle B\!\,}$ and the initial point of ${\displaystyle A\!\,}$,

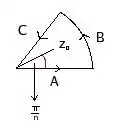
where ${\displaystyle R\!\,}$ is a fixed positive number such that

the pole ${\displaystyle z_{0}=e^{i{\frac {\pi }{n}}}\!\,}$ is inside the curve ${\displaystyle \gamma \!\,}$. Then , we need to estimate the integral

${\displaystyle \int _{\gamma }f(z)=\underbrace {\int _{0}^{R}f(z)} _{A}+\underbrace {\int _{S(R)}f(z)} _{B}+\underbrace {\int _{Re^{i{\frac {2\pi }{n}}}}^{0}f(z)} _{C}\!\,}$

Compute Residues of f at z0= exp{i\pi /n}

${\displaystyle {\begin{aligned}Res(f,z_{0})&=\left.{\frac {1}{(z^{n}+1)'}}\right|_{z=z_{0}}\\&={\frac {1}{nz_{0}^{n-1}}}\\&={\frac {1}{ne^{{\frac {i\pi }{n}}(n-1)}}}\\&={\frac {e^{\frac {i\pi }{n}}}{ne^{i\pi }}}\\&={\frac {-1}{n}}e^{\frac {i\pi }{n}}\end{aligned}}\!\,}$

Bound Arc Portion (B) of Integral

${\displaystyle {\begin{aligned}|B|&=\left|\int _{S(R)}{\frac {dz}{z^{n}+1}}\right|\\&\leq \int _{S(R)}{\frac {dz}{|z^{n}+1|}}\\&=\int _{S(R)}{\frac {dz}{|R^{n}+1|}}\\&\leq {\frac {1}{R^{n}}}\int _{S(R)}dz\\&={\frac {1}{R^{n}}}{\frac {2\pi }{n}}R\\&={\frac {2\pi }{nR^{n-1}}}\end{aligned}}}$

Hence as ${\displaystyle R\rightarrow \infty \!\,}$, ${\displaystyle |B|\rightarrow 0\!\,}$

Parametrize (C) in terms of (A)

Let ${\displaystyle z=re^{i{\frac {2\pi }{n}}}\!\,}$ where ${\displaystyle r\!\,}$ is real number. Then ${\displaystyle dz=e^{i{\frac {2\pi }{n}}}dr\!\,}$

${\displaystyle {\begin{aligned}C&=\int _{Re^{i{\frac {2\pi }{n}}}}^{0}{\frac {dz}{1+z^{n}}}\\&=-\int _{0}^{Re^{i{\frac {2\pi }{n}}}}{\frac {dz}{1+z^{n}}}\\&=-\int _{0}^{R}{\frac {e^{i{\frac {2\pi }{n}}}}{1+(re^{i{\frac {2\pi }{n}}})^{n}}}\\&=-\int _{0}^{R}{\frac {e^{i{\frac {2\pi }{n}}}}{1+r^{n}}}\\&=-e^{i{\frac {2\pi }{n}}}\underbrace {\int _{0}^{R}{\frac {dr}{1+r^{n}}}} _{A}\\\end{aligned}}}$

Apply Cauchy Integral Formula

From Cauchy Integral Formula, we have,

${\displaystyle A+B+C=2\pi i{\frac {-e^{i{\frac {\pi }{n}}}}{n}}\!\,}$

As ${\displaystyle R\rightarrow \infty \!\,}$, ${\displaystyle B\rightarrow 0\!\,}$. Also ${\displaystyle C\!\,}$ can be written in terms of ${\displaystyle A\!\,}$. Hence

${\displaystyle {\begin{aligned}A+B+C&=A+C\\&=(1-e^{i{\frac {2\pi }{n}}})A\end{aligned}}}$

We then have,

${\displaystyle {\begin{aligned}A&={\frac {2\pi i}{n}}{\frac {e^{i{\frac {\pi }{n}}}}{e^{i{\frac {2\pi }{n}}}-1}}\\&={\frac {\pi }{n}}{\frac {2ie^{i{\frac {\pi }{n}}}}{e^{i{\frac {\pi }{n}}}(e^{i{\frac {\pi }{n}}}-e^{-i{\frac {\pi }{n}}})}}\\&={\frac {\pi }{n}}{\frac {1}{\sin({\frac {\pi }{n}})}}\end{aligned}}}$

Lemma: Two fixed points imply identity

Lemma. Let ${\displaystyle f\!\,}$ be analytic on the unit ${\displaystyle D\!\,}$, and assume that ${\displaystyle |f(z)|<1\!\,}$ on the disc. Prove that if there exist two distinct points ${\displaystyle a\!\,}$ and ${\displaystyle b\!\,}$ in the disc which are fixed points, that is, ${\displaystyle f(a)=a\!\,}$ and ${\displaystyle f(b)=b\!\,}$, then ${\displaystyle f(z)=z\!\,}$.

Proof Let ${\displaystyle h:D\rightarrow D\!\,}$ be the automorphism defined as

${\displaystyle h(z)={\frac {a-z}{1-{\overline {a}}z}}\!\,}$

Consider now ${\displaystyle F(z)=h\circ f\circ h^{-1}(z)\!\,}$. Then, F has two fixed points, namely

${\displaystyle F(0)=h\circ f\circ h^{-1}(0)=h\circ f(a)=h(a)=0\!\,}$

${\displaystyle F\left({\frac {a-b}{1-{\overline {a}}b}}\right)=h\circ f\circ h^{-1}\left({\frac {a-b}{1-{\overline {a}}b}}\right)=h\circ f(b)=h(b)={\frac {a-b}{1-{\overline {a}}b}}\!\,}$.

Since ${\displaystyle F(0)=0\!\,}$,

${\displaystyle {\frac {a-b}{1-{\overline {a}}b}}\neq 0\!\,}$ (since ${\displaystyle a\!\,}$ is different to ${\displaystyle b\!\,}$), and

${\displaystyle \left|F\left({\frac {a-b}{1-{\overline {a}}b}}\right)\right|=\left|{\frac {a-b}{1-{\overline {a}}b}}\right|\!\,}$,

by Schwarz Lemma,

${\displaystyle F(z)=\alpha z\!\,}$.

But, replacing ${\displaystyle {\frac {a-b}{1-{\overline {a}}b}}\!\,}$ into the last formula, we get ${\displaystyle \alpha =1\!\,}$.

Therefore,

${\displaystyle h\circ f\circ h^{-1}(z)=z\!\,}$,

which implies

${\displaystyle f(z)=z\!\,}$

Shift Points to Create Fixed Points

Let ${\displaystyle f(z)=g(z)-1\!\,}$. Then ${\displaystyle f(0)=0\!\,}$ and ${\displaystyle f(-1)=-1\!\,}$.

Notice that ${\displaystyle S\!\,}$ is an infinite horizontal strip centered around the real axis with height ${\displaystyle \pi \!\,}$. Since ${\displaystyle f(z)\!\,}$ is a unit horizontal shift left, ${\displaystyle f(S)\subset S\!\,}$.

Use Riemann Mapping Theorem

From the Riemann mapping theorem, there exists a biholomorphic (bijective and holomorphic) mapping ${\displaystyle h\!\,}$, from the open unit disk ${\displaystyle D\!\,}$ to ${\displaystyle S\!\,}$.

Define Composition Function

Let ${\displaystyle F=h^{-1}\circ f\circ h\!\,}$. Then ${\displaystyle F\!\,}$ maps ${\displaystyle D\!\,}$ to ${\displaystyle D\!\,}$.

From the lemma, since ${\displaystyle F(z)\!\,}$ has two fixed points, ${\displaystyle F(z)=z\!\,}$ which implies ${\displaystyle f(z)=z\!\,}$ which implies ${\displaystyle g=z+1\!\,}$.

Choose any compact set K in D

Choose any compact set ${\displaystyle K\!\,}$ in the open unit disk ${\displaystyle D\!\,}$. Since ${\displaystyle K\!\,}$ is compact, it is also closed and bounded.

We want to show that for all ${\displaystyle f\in {\mathcal {F}}\!\,}$ and all ${\displaystyle z\in K\!\,}$, ${\displaystyle |f(z)|\!\,}$ is bounded i.e.

${\displaystyle |f(z)|<B_{K}\!\,}$

where ${\displaystyle B_{K}\!\,}$ is some constant dependent on the choice of ${\displaystyle K\!\,}$.

Apply Maximum Modulus Principle to find |f(z0)|

Choose ${\displaystyle z_{0}\!\,}$ that is the shortest distance from the boundary of the unit disk ${\displaystyle D\!\,}$. From the maximum modulus principle, ${\displaystyle |f(z_{0})|=\max _{z\in K}|f(z|\!\,}$.

Note that ${\displaystyle z_{0}\!\,}$ is independent of the choice of ${\displaystyle f\in {\mathcal {F}}\!\,}$.

Apply Cauchy's Integral Formula to f^2(z0)

We will apply Cauchy's Integral formula to ${\displaystyle f^{2}(z_{0})\!\,}$ (instead of ${\displaystyle f(z_{0})\!\,}$) to take advantage of the hypothesis.

Choose sufficiently small ${\displaystyle r_{0}>0\!\,}$ so that ${\displaystyle D(z_{0},r_{0})\!\,\in D}$

${\displaystyle {\begin{aligned}f^{2}(z_{0})&={\frac {1}{2\pi i}}\int _{|z-z_{0}|=r_{0}}{\frac {f^{2}(z)}{z-z_{0}}}dz\\&={\frac {1}{2\pi i}}\int _{0}^{2\pi }{\frac {f^{2}(z_{0}+r_{0}e^{i\theta })ir_{0}e^{i\theta }}{(z_{0}+r_{0}e^{i\theta })-z_{0}}}d\theta \\&={\frac {1}{2\pi }}\int _{0}^{2\pi }f^{2}(z_{0}+r_{0}e^{i\theta })d\theta \end{aligned}}}$

Integrate with respect to r

${\displaystyle {\begin{aligned}\int _{0}^{r_{0}}rf^{2}(z_{0})dr&=\int _{0}^{r_{0}}\int _{0}^{2\pi }f^{2}(z_{0}+re^{i\theta })rdrd\theta \\&={\frac {1}{2\pi }}\int \int _{D(z_{0},r)}f^{2}(x+iy)dxdy\end{aligned}}}$

Integrating the left hand side, we have

${\displaystyle \int _{0}^{r_{0}}rf^{2}(z_{0})dr={\frac {r_{0}^{2}}{2}}f^{2}(z_{0})\!\,}$

Hence,

${\displaystyle {\frac {r_{0}^{2}}{2}}f^{2}(z_{0})={\frac {1}{2\pi }}\int \int _{D(z_{0},r)}f^{2}(x+iy)dxdy\!\,}$

Bound |f(z0)| by using hypothesis

${\displaystyle {\begin{aligned}\left|{\frac {r_{0}^{2}}{2}}f^{2}(z_{0})\right|&=\left|{\frac {1}{2\pi }}\int \int _{D(z_{0},r_{0})}f^{2}(x+iy)dxdy\right|\\&\leq {\frac {1}{2\pi }}\int \int _{D(z_{0},r_{0})}|f^{2}(x+iy)|dxdy\\&\leq {\frac {1}{2\pi }}\int \int _{D}|f^{2}(x+iy)|dxdy\\&\leq {\frac {1}{2\pi }}\\\\{\mbox{Then }}\\\left|{\frac {r_{0}^{2}}{2}}f^{2}(z_{0})\right|&\leq {\frac {1}{2\pi }}\\\\{\mbox{This implies}}\\\\|f(z_{0})|&\leq {\frac {1}{r_{0}{\sqrt {\pi }}}}\end{aligned}}}$

Apply Montel's Theorem

Then, since any ${\displaystyle f\in {\mathcal {F}}\!\,}$ is uniformly bounded in every compact set, by Montel's Theorem, it follows that ${\displaystyle {\mathcal {F}}\!\,}$ is normal