< Statistics < Distributions
Continuous Uniform Distribution
Probability density function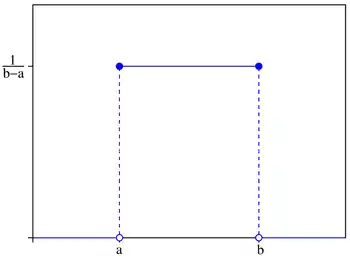 Using maximum convention | |
Cumulative distribution function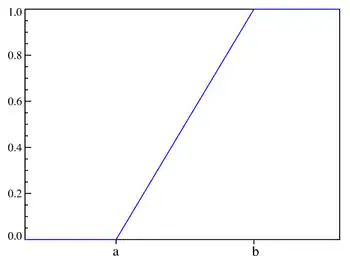 | |
| Notation | |
|---|---|
| Parameters | |
| Support | |
| CDF | |
| Mean | |
| Median | |
| Mode | any value in |
| Variance | |
| Skewness | 0 |
| Ex. kurtosis | |
| Entropy | |
| MGF | |
| CF | |
The (continuous) uniform distribution, as its name suggests, is a distribution with probability densities that are the same at each point in an interval. In casual terms, the uniform distribution shapes like a rectangle.
Mathematically speaking, the probability density function of the uniform distribution is defined as
And the cumulative distribution function is:
Mean
We derive the mean as follows.
As the uniform distribution is 0 everywhere but [a, b] we can restrict ourselves that interval
Variance
We use the following formula for the variance.
External links
This article is issued from Wikibooks. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.