Vectors

Scalars vs Vectors

Scalars are numbers, or quantities which represent numbers, such as ${\displaystyle 7,x,y,e,\pi ,...}$

Vectors are composed of a direction and a magnitude, or multiple scalar components, such as ${\displaystyle \left\langle 3,4\right\rangle ,5{\hat {i}},3{\hat {i}}+4{\hat {j}},...}$ The magnitude of a vector is found with the Pythagorean theorem, ${\displaystyle \left\Vert {\vec {a}}\right\|={\sqrt {a_{x}^{2}+a_{y}^{2}}}}$

Vector Multiplication

Dot Product

a depiction of the relationship between the angle ${\displaystyle \theta }$, the vectors ${\displaystyle {\vec {x}}}$ and ${\displaystyle {\vec {y}}}$, and the dot product ${\displaystyle {\vec {x}}\cdot {\vec {y}}}$

The Dot Product (or Scalar Product) of two vectors is given by ${\displaystyle \left\langle a,b\right\rangle \,\cdot \,\left\langle c,d\right\rangle =a\,c+b\,d}$. The dot product is equal to the cosine of the angle between the vectors, multiplied by the product of their magnitudes, and therefore the angle between the vectors can easily be calculated using ${\displaystyle \cos {(\theta )}={\frac {{\vec {a}}\cdot {\vec {b}}}{\left\Vert {\vec {a}}\right\|\,\left\Vert {\vec {b}}\right\|}}}$

Cross Product

A depiction of the cross product of vectors ${\displaystyle {\vec {u}}}$ and ${\displaystyle {\vec {v}}}$.

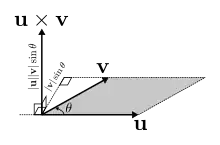
The Cross Product of two vectors results in another vector, normal to both initial vectors. The magnitude of the cross product is equal to the area of the parallelogram formed by the two vectors, or ${\displaystyle \left\Vert {\vec {a}}\times {\vec {b}}\right\|=\left\Vert {\vec {a}}\right\|\,\left\Vert {\vec {b}}\right\|\,\sin {(\theta )}}$