Practical Electronics/Parallel RC

Parallel RC

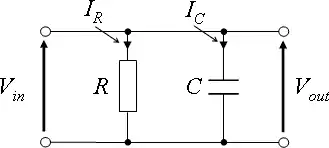
Circuit Impedance

{\frac {1}{Z}}={\frac {1}{Z_{R}}}+{\frac {1}{Z_{C}}}

{\frac {1}{Z}}={\frac {1}{R}}+j\omega C={\frac {j\omega CR+1}{R}}

Z=R{\frac {1}{j\omega CR+1}}

Circuit Response

I=I_{R}+I_{C}

I={\frac {V}{R}}+C{\frac {dV}{dt}}

V=(IR-RC{\frac {dV}{dt}})

Parallel RL

\

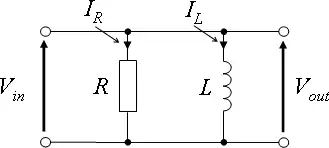
Circuit Impedance

{\frac {1}{Z}}={\frac {1}{Z_{R}}}+{\frac {1}{Z_{L}}}

{\frac {1}{Z}}={\frac {1}{R}}+{\frac {1}{j\omega L}}={\frac {R+j\omega L}{j\omega RL}}

Z={\frac {j\omega RL}{R+j\omega L}}=j\omega L{\frac {1}{1+j\omega {\frac {L}{R}}}}

Circuit Response

I=I_{R}+I_{L}

I={\frac {V}{R}}+{\frac {1}{L}}\int Vdt

V=IR-{\frac {R}{L}}\int Vdt

Parallel LC

Circuit Impedance

{\frac {1}{Z}}={\frac {1}{Z_{L}}}+{\frac {1}{Z_{C}}}

{\frac {1}{Z}}={\frac {1}{j\omega L}}+j\omega C={\frac {(j\omega )^{2}LC+1}{j\omega L}}

Z={\frac {j\omega L}{(j\omega )^{2}LC+1}}

Circuit response

I=I_{L}+I_{C}

I={\frac {1}{L}}\int Vdt+C{\frac {dV}{dt}}

Parallel RLC

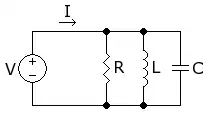
Circuit Impedance

{\frac {1}{Z}}={\frac {1}{Z_{R}}}+{\frac {1}{Z_{L}}}+{\frac {1}{Z_{C}}}

{\frac {1}{Z}}={\frac {1}{R}}+{\frac {1}{j\omega L}}+j\omega C

{\frac {1}{Z}}={\frac {(j\omega )^{2}RLC+j\omega L+R}{j\omega RL}}

{\frac {1}{Z}}={\frac {(j\omega )^{2}LC+j\omega {\frac {L}{R}}+1}{j\omega L}}

Circuit response

I=I_{R}+I_{L}+I_{C}

I={\frac {V}{R}}+{\frac {1}{L}}\int Vdt+C{\frac {dV}{dt}}

I={\frac {V}{R}}+{\frac {1}{L}}\int Vdt+C{\frac {dV}{dt}}

V=IR-{\frac {R}{L}}\int Vdt-CR{\frac {dV}{dt}}

Natural Respond

0={\frac {V}{R}}+{\frac {1}{L}}\int Vdt+C{\frac {dV}{dt}}

Forced Respond

I_{t}=IR+L{\frac {dI}{dt}}+{\frac {1}{C}}\int Idt

Second ordered equation that has two roots

ω = -α ± ${\sqrt {\alpha ^{2}-\beta ^{2}}}$

Where

$\alpha ={\frac {R}{2L}}$
$\beta ={\frac {1}{\sqrt {LC}}}$

The current of the network is given by

A e^{ω1 t} + B e^{ω2 t}

From above

When

{\alpha ^{2}=\beta ^{2}}

, there is only one real root

ω = -α

When

{\alpha ^{2}>\beta ^{2}}

, there are two real roots

ω = -α ±

{\sqrt {\alpha ^{2}-\beta ^{2}}}

When

{\alpha ^{2}<\beta ^{2}}

, there are two complex roots

ω = -α ± j

{\sqrt {\beta ^{2}-\alpha ^{2}}}

Resonance Response

At resonance, the impedance of the frequency dependent components cancel out . Therefore the net voltage of the circui is zero

$Z_{L}-Z_{C}=0$ and $V_{L}+V_{C}=0$

\omega L={\frac {1}{\omega C}}

\omega ={\sqrt {\frac {1}{LC}}}

Z=Z_{R}+(Z_{L}-Z_{C})=Z_{R}=R

I={\frac {V}{R}}

At Resonance Frequency

\omega ={\sqrt {\frac {1}{LC}}}

.

I={\frac {V}{R}}

. Current is at its maximum value

Further analyse the circuit

At ω = 0, Capacitor Opened circuit . Therefore, I = 0 .

At ω = 00, Inductor Opened circuit . Therefore, I = 0 .

With the values of Current at three ω = 0 , ${\sqrt {\frac {1}{LC}}}$ , 00 we have the plot of I versus ω . From the plot If current is reduced to halved of the value of peak current $I={\frac {V}{2R}}$ , this current value is stable over a Frequency Band ω₁ - ω₂ where ω₁ = ω_o - Δω, ω₂ = ω_o + Δω

In RLC series, it is possible to have a band of frequencies where current is stable, ie. current does not change with frequency . For a wide band of frequencies respond, current must be reduced from it's peak value . The more current is reduced, the wider the bandwidth . Therefore, this network can be used as Tuned Selected Band Pass Filter . If tune either L or C to the resonance frequency $\omega ={\sqrt {\frac {1}{LC}}}$ . Current is at its maximum value $I={\frac {V}{R}}$ . Then, adjust the value of R to have a value less than the peak current $I={\frac {V}{R}}$ by increasing R to have a desired frequency band .

If R is increased from R to 2R then the current now is $I={\frac {V}{2R}}$ which is stable over a band of frequency

ω₁ - ω₂ where

ω₁ = ω_o - Δω

ω₂ = ω_o + Δω

For value of I < $I={\frac {V}{2R}}$ . The circuit respond to Wide Band of frequencies . For value of $I={\frac {V}{R}}$ < I > $I={\frac {V}{2R}}$ . The circuit respond to Narrow Band of frequencies

Summary

Circuit	Symbol	Series	Parallel
RC		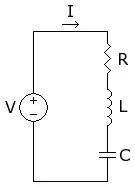	A parallel RC Circuit
Impedance	Z	$Z_{t}=R+{\frac {1}{\omega C}}={\frac {\omega CR+1}{\omega C}}$	${\frac {1}{Z_{t}}}={\frac {1}{Z_{R}}}+{\frac {1}{Z_{C}}}={\frac {1}{R}}+\omega C={\frac {R}{\omega CR+1}}$
Frequency	$\omega _{o}=2f_{o}$	$Z_{R}=Z_{C}$ $R={\frac {1}{\omega C}}$ $\omega ={\frac {1}{CR}}$	${\frac {1}{R}}={\frac {1}{\omega C}}$ ${\frac {1}{R}}=\omega C$ $\omega ={\frac {1}{CR}}$
Voltage	V	$V=IR+{\frac {1}{C}}\int Idt$	$I={\frac {V}{R}}+C{\frac {dV}{dt}}$
Current	I	$\int Idt=C(V-IR)$	${\frac {dV}{dt}}={\frac {1}{C}}(I-{\frac {V}{R}})$
Phase Angle		Tan θ = 1/2πf RC f = 1/2π Tan CR t = 2π Tan CR	Tan θ = 1/2πf RC f = 1/2π Tan CR t = 2π Tan CR

This article is issued from Wikibooks. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.