A Green's function for a linear operator ${\displaystyle L}$ over ${\displaystyle \mathbb {R} }$ is a real function ${\displaystyle g}$ such that ${\displaystyle Lx=y}$ is solved by ${\displaystyle x=g*y}$; where ${\displaystyle *}$ symbolizes convolution. Hence, ${\displaystyle L(g*y)=y}$ so that ${\displaystyle g*y}$ is a right inverse of ${\displaystyle L}$ and ${\displaystyle g*}$ is a particular solution to the inhomogeneous equation.

For example: ${\displaystyle ({\tfrac {d}{dt}})^{2}x+x=f}$ is solved by ${\displaystyle x=\sin *f=\int _{0}^{t}sin(t-\tau )f(\tau )d\tau }$

Such a function might not exist and when it does might not be unique. The conditions under which this method is valid require careful examination. However, the theory of Green's functions obtains a more complete and regular form over the theory of distributions, or generalized functions.

As will be seen, the theory of Green's functions provides an extremely elegant procedure of solving differential equations. We wish to present here this method on a rigorous foundation.

The Dirac delta-function

The Dirac delta-function ${\displaystyle \delta (x)}$is not a function as it is ordinarily defined. However, we write it as if it were a function, keeping in mind the scope of the definition.

For any function ${\displaystyle f:\mathbb {R} \to \mathbb {R} }$,we define

${\displaystyle \int _{-\infty }^{\infty }f(x)\delta (x)dx=f(0)}$ but for every ${\displaystyle \epsilon >0}$,

${\displaystyle \int _{-\infty }^{-\epsilon }f(x)\delta (x)dx=\int _{\epsilon }^{\infty }f(x)\delta (x)dx=0}$

It follows that ${\displaystyle \int _{-\infty }^{\infty }\delta (x)dx=1}$

These conditions seem to be satisfied by a "function" ${\displaystyle \delta (x)}$ which has value zero whenever ${\displaystyle x\neq 0}$, but has "infinite" value at ${\displaystyle x=0}$

Approximations

There are a few ways to approximate the delta function in terms of sequences ordinary functions. We give two examples

The Boxcar function

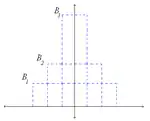
The boxcar function ${\displaystyle B_{n}:\mathbb {R} \to \{0,1\}}$ such that

${\displaystyle B_{n}(x)={\begin{cases}0&|x|>{\tfrac {1}{2n}}\\1&|x|\leq {\tfrac {1}{2n}}\end{cases}}}$

We can see that the sequence ${\displaystyle \left\langle B_{n}\right\rangle }$ represents an approximation to the delta function.

The bell curve

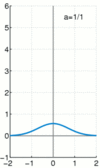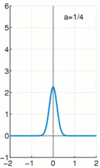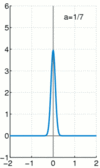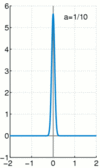
The delta function can also be approximated by the ubiquitous Gaussian.

We write ${\displaystyle G_{n}(x)={\frac {n}{\sqrt {\pi }}}\mathrm {e} ^{-x^{2}n^{2}}}$

Green's function

Consider an equation of the type ${\displaystyle {\mathcal {L}}u(x)=F(x)}$...(1), where ${\displaystyle {\mathcal {L}}}$ is a differential operator. The functions ${\displaystyle u,F}$ may in general be functions of several independents, but for sake of clarity, we will write them here as if they were real valued. In most cases of interest, this equation can be written in the form

${\displaystyle a(x){\frac {d^{2}u}{dx^{2}}}+b(x){\frac {du}{dx}}+c(x)=F(x)}$ to be solved for ${\displaystyle u(x)}$ in some closed set ${\displaystyle A}$, with ${\displaystyle a(x)}$ being non-zero over ${\displaystyle A}$

Now, it so happens, that in problems of physics, it is much more convenient to solve the equation ${\displaystyle {\mathcal {L}}u(x)=f(x)}$, when ${\displaystyle f}$ is the delta function ${\displaystyle f(x)=\delta (x-x_{0})}$.

In this case, the solution of the operator ${\displaystyle {\mathcal {L}}}$ is called the Green's function ${\displaystyle G(x,x_{0})}$. That is,

${\displaystyle {\mathcal {L}}G(x,x_{0})=\delta (x-x_{0})}$

Now, by the definition of the delta-function, we have that ${\displaystyle F(x)=\int _{-\infty }^{\infty }F(x')\delta (x'-x)dx}$, where ${\displaystyle F(x')}$ act as "weights" to the delta function.

Hence, we have, ${\displaystyle {\mathcal {L}}u(x)=\int _{-\infty }^{\infty }F(x'){\mathcal {L}}G(x,x')dx}$

Note here that${\displaystyle {\mathcal {L}}}$ is an operator that depends on ${\displaystyle x}$ but not ${\displaystyle x'}$. Thus,

${\displaystyle {\mathcal {L}}u(x)={\mathcal {L}}\int _{-\infty }^{\infty }F(x')G(x,x')dx}$. We can view this as anologous to the inversion of ${\displaystyle {\mathcal {L}}}$ and hence, we write

${\displaystyle u_{p}(x)=\int _{-\infty }^{\infty }F(x')G(x,x')dx}$

The subscript ${\displaystyle p}$ denotes that we have found a particular solution among the many possible. For example, consider any harmonic solution ${\displaystyle {\mathcal {L}}u_{h}(x)=0}$.

If we add ${\displaystyle u'(x)=u_{h}(x)+u_{p}(x)}$, we see that ${\displaystyle u'(x)}$ is still a solution of (1). Thus, we have a class of functions satisfying (1).

Green's functions from eigenfunctions

Consider the eigenvalues ${\displaystyle \lambda _{n}}$ and the corresponding eigenfunctions ${\displaystyle \phi _{n}}$ of the differential operator ${\displaystyle {\mathcal {L}}}$, that is ${\displaystyle {\mathcal {L}}\phi _{n}=\lambda _{n}\phi _{n}}$

Without loss of generality, we assume that these eigenfunctions are orthogonal. Further, we assume that they form a basis.

Thus, we can write ${\displaystyle u(x)=\sum _{i=1}^{n}\alpha _{i}\phi _{i}}$ and ${\displaystyle F(x)=\sum _{i=1}^{n}\beta _{i}\phi _{i}}$.

Now ${\displaystyle {\mathcal {L}}u(x)={\mathcal {L}}\sum _{i=1}^{n}\alpha _{i}\phi _{i}=\sum _{i=1}^{n}\alpha _{i}{\mathcal {L}}\phi _{i}=\sum _{i=1}^{n}\alpha _{i}\lambda _{i}\phi _{i}=\sum _{i=1}^{n}\beta _{i}\phi _{i}=F(x)}$ and hence, ${\displaystyle \alpha _{i}={\frac {\beta _{i}}{\lambda _{i}}}}$

by definition of orthogonality, ${\displaystyle \beta _{n}=\int _{-\infty }^{\infty }F(x)\phi _{n}(x)dx=(F(x)\cdot \phi _{n}(x))}$

Now, ${\displaystyle u(x)=\sum _{i=1}^{n}\alpha _{i}\phi _{i}(x)=\sum _{i=1}^{n}{\frac {\beta _{i}}{\lambda _{i}}}\phi _{i}(x)=\sum _{i=1}^{n}{\frac {(F(x')\cdot \phi _{i}(x'))}{\lambda _{i}}}\phi _{i}}$

and hence, we can write the Green's function as ${\displaystyle G(x,x')=\sum _{i=1}^{n}{\frac {\phi _{i}(x)\phi _{i}(x')}{\lambda _{i}}}}$