Engineering Acoustics/Simple Oscillation

< Engineering Acoustics

The Position Equation

This section shows how to form the equation describing the position of a mass on a spring.

For a simple oscillator consisting of a mass m attached to one end of a spring with a spring constant s, the restoring force, f, can be expressed by the equation

f=-sx\,

where x is the displacement of the mass from its rest position. Substituting the expression for f into the linear momentum equation,

f=ma=m{d^{2}x \over dt^{2}}\,

where a is the acceleration of the mass, we can get

m{\frac {d^{2}x}{dt^{2}}}=-sx

or,

{\frac {d^{2}x}{dt^{2}}}+{\frac {s}{m}}x=0

Note that the frequency of oscillation $\omega _{0}$ is given by

\omega _{0}^{2}={s \over m}\,

To solve the equation, we can assume

x(t)=Ae^{\lambda t}\,

The force equation then becomes

(\lambda ^{2}+\omega _{0}^{2})Ae^{\lambda t}=0,

Giving the equation

\lambda ^{2}+\omega _{0}^{2}=0,

Solving for $\lambda$

\lambda =\pm j\omega _{0}\,

This gives the equation of x to be

x=C_{1}e^{j\omega _{0}t}+C_{2}e^{-j\omega _{0}t}\,

Note that

j=(-1)^{1/2}\,

and that C₁ and C₂ are constants given by the initial conditions of the system

If the position of the mass at t = 0 is denoted as x₀, then

C_{1}+C_{2}=x_{0}\,

and if the velocity of the mass at t = 0 is denoted as u₀, then

-j(u_{0}/\omega _{0})=C_{1}-C_{2}\,

Solving the two boundary condition equations gives

C_{1}={\frac {1}{2}}(x_{0}-j(u_{0}/\omega _{0}))

C_{2}={\frac {1}{2}}(x_{0}+j(u_{0}/\omega _{0}))

The position is then given by

$x(t)=x_{0}cos(\omega _{0}t)+(u_{0}/\omega _{0})sin(\omega _{0}t)\,$

This equation can also be found by assuming that x is of the form

x(t)=A_{1}cos(\omega _{0}t)+A_{2}sin(\omega _{0}t)\,

And by applying the same initial conditions,

A_{1}=x_{0}\,

A_{2}={\frac {u_{0}}{\omega _{0}}}\,

This gives rise to the same position equation

x(t)=x_{0}cos(\omega _{0}t)+(u_{0}/\omega _{0})sin(\omega _{0}t)\,

Back to Main page

Alternate Position Equation Forms

If A₁ and A₂ are of the form

A_{1}=Acos(\phi )\,

A_{2}=Asin(\phi )\,

Then the position equation can be written

$x(t)=Acos(\omega _{0}t-\phi )\,$

By applying the initial conditions (x(0)=x₀, u(0)=u₀) it is found that

x_{0}=Acos(\phi )\,

{\frac {u_{0}}{\omega _{0}}}=Asin(\phi )\,

If these two equations are squared and summed, then it is found that

$A={\sqrt {x_{0}^{2}+({\frac {u_{0}}{\omega _{0}}})^{2}}}\,$

And if the difference of the same two equations is found, the result is that

$\phi =tan^{-1}({\frac {u_{0}}{x_{0}\omega _{0}}})\,$

The position equation can also be written as the Real part of the imaginary position equation

\mathbf {Re} [x(t)]=x(t)=Acos(\omega _{0}t-\phi )\,

Due to euler's rule (e^jφ = cosφ + jsinφ), x(t) is of the form

x(t)=Ae^{j(\omega _{0}t-\phi )}\,

Example 1.1

GIVEN: Two springs of stiffness, $s$ , and two bodies of mass, $M$

FIND: The natural frequencies of the systems sketched below

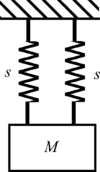Simple Oscillator-1.2.1.a

$s_{TOTAL}=s+s{\text{ (springs are in parallel)}}$

$\omega _{0}={\sqrt {\frac {s_{TOTAL}}{m_{TOTAL}}}}={\sqrt {\frac {2s}{M}}}$

$\mathbf {f_{0}} ={\frac {\omega _{0}}{2\pi }}=\mathbf {{\frac {1}{2\pi }}{\sqrt {\frac {2s}{M}}}}$

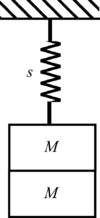Simple Oscillator-1.2.1.b

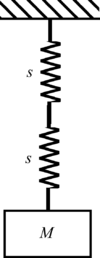$\omega _{0}={\sqrt {\frac {s_{TOTAL}}{m_{TOTAL}}}}={\sqrt {\frac {s}{2M}}}$

$\mathbf {f_{0}} ={\frac {\omega _{0}}{2\pi }}=\mathbf {{\frac {1}{2\pi }}{\sqrt {\frac {s}{2M}}}}$

Simple Oscillator-1.2.1.c

$\mathbf {1.} {\text{ }}s(x_{1}-x_{2})=sx_{2}$

$\mathbf {2.} {\text{ }}-s(x_{1}-x_{2})=m{\frac {d^{2}x}{dt^{2}}}$

${\frac {d^{2}x_{1}}{dt^{2}}}+{\frac {s}{2m}}x_{1}=0$

$\omega _{0}={\sqrt {\frac {s}{2m}}}$

$\mathbf {f_{0}={\frac {1}{2\pi }}{\sqrt {\frac {s}{2m}}}}$

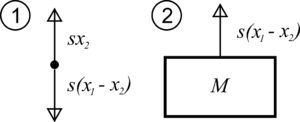
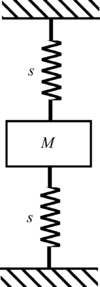Simple Oscillator-1.2.1.d

$\omega _{0}={\sqrt {\frac {2s}{m}}}$

$\mathbf {f_{0}={\frac {1}{2\pi }}{\sqrt {\frac {2s}{m}}}}$

Back to Main page

This article is issued from Wikibooks. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.