example 2nd order circuit with two inductors and two resistors .. solved using the convolution integral in wikibook circuit analysis

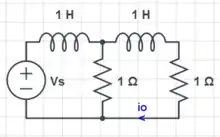
Given that V_s = (1 + 2t)μ(t), find i_o using the convolution integral.

Transfer function

${\displaystyle H(s)={\frac {\mathbb {I} _{o}}{\mathbb {V} _{s}}}={\frac {\mathbb {I} _{T}}{\mathbb {V} _{s}}}*{\frac {\mathbb {I} _{o}}{\mathbb {I} _{T}}}={\frac {1}{s+{\frac {1}{1+{\frac {1}{1+s}}}}}}*{\frac {\frac {1}{1+s}}{1+{\frac {1}{1+s}}}}}$

simplify((1/(1+s))/((s+1/(1+1/(1+s)))*(1 + 1/(1 + s))))

${\displaystyle H(s)={\frac {1}{s^{2}+3s+1}}}$

solve(s^2 + 3*s + 1,s)

Homogeneous Solution

Two real, different roots:

${\displaystyle s_{1,2}={\frac {-3\pm {\sqrt {5}}}{2}}}$

So I_o has this form:

${\displaystyle i_{o}(t)=Ae^{s_{1}t}+Be^{s_{2}t}}$

Particular Solution

After a very long time, inductors are shorts, the voltage across both 1 ohm resistors is 1 volt, so i_o is 1 amp:

${\displaystyle i_{o_{p}}(t)=1}$

Initial Conditions

Adding the particular and homogeneous solutions together, have this form:

${\displaystyle i_{o}(t)=1+Ae^{s_{1}t}+Be^{s_{2}t}+C_{1}}$

After a long period of time (using the particular initial condition again), the current is going to be 1:

${\displaystyle i_{o}(\infty )=1+C_{1}=1}$

${\displaystyle C_{1}=0}$

Initially, the two inductors are going to be opens, thus i_o has to be 0:

${\displaystyle i_{o}(0)=0=1+A+B}$

Initially, all the drop is going to be across the first inductor, leaving the voltage across the second zero. The current i_o flows through both the second inductor and it's serial resistor, so an equation for this voltage can be obtained by taking the derivative:

${\displaystyle V_{L}(t)=L{di_{o}(t) \over dt}=s_{1}Ae^{s_{1}t}+s_{2}Be^{s_{2}t}}$

${\displaystyle V_{L}(0)=0=s_{1}A+s_{2}B}$

solve([1+A+B,s1*A + s2*B],[A,B])

${\displaystyle A={\frac {s_{2}}{s_{1}-s_{2}}}}$

${\displaystyle B=-{\frac {s_{1}}{s_{1}-s_{2}}}}$

So:

${\displaystyle i_{0}(t)=1+{\frac {s_{2}e^{s_{1}t}-s_{1}e^{s_{2}t}}{s_{1}-s_{2}}}}$

Impulse Solution

Taking the derivative of the above get:

${\displaystyle i_{o_{\delta }}(t)={\frac {s_{1}s_{2}}{s_{1}-s_{2}}}(e^{s_{1}t}-e^{s_{2}t})}$

Convolution Integral

${\displaystyle i_{o}(t)=\int _{0}^{t}{\frac {s_{1}s_{2}}{s_{1}-s_{2}}}(e^{s_{1}t}-e^{s_{2}t})*(1+2x)dx}$

syms t x
s1 = (-3 + sqrt(5))/2;
s2 = (-3 - sqrt(5))/2;
f = (s1*s2/(s1-s2)*(exp(s1*(t-x))-exp(s2*(t-x)))*(1+2*x));
S =int(f,0,t);
vpa(S, 3)

${\displaystyle i_{o}(t)=2t+4.96e^{-0.382t}+0.0403e^{-2.62t}-5+C_{1}}$

At t=0:

${\displaystyle i_{o}(0)=0=4.96+.04-5+C_{1}}$

Which means that C_1 = 0 so finally:

${\displaystyle i_{o}(t)=2t+4.96e^{-0.382t}+0.0403e^{-2.62t}-5}$