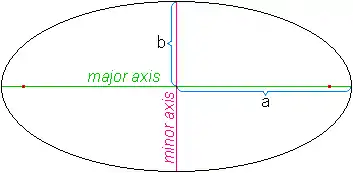
An ellipse is the collection of points that are equidistant from two points, called foci (singular focus).

The foci are found on the major axis, which has a length of 2a. The minor axis is 2b, and is smaller.

The "roundness" or "longness" of an ellipse can be measured by eccentricity. If c is the distance from the center to a focus, then e = c / a.

The latus rectum is a line parallel to the minor axis that crosses through a focus. Its length is b² / a.

"Long" ellipses are generally written as

${\displaystyle {\frac {(x-h)^{2}}{a^{2}}}+{\frac {(y-k)^{2}}{b^{2}}}=1}$

where (h,k) is the center, while "tall" ellipses are written as

${\displaystyle {\frac {(y-k)^{2}}{a^{2}}}+{\frac {(x-h)^{2}}{b^{2}}}=1}$

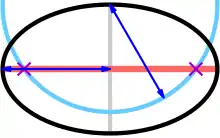
A method to locate the foci of any ellipse: the foci (purple crosses) are at intersects of the major axis (red) and a circle (cyan) of radius equal to the semi-major axis (blue), centred on an end of the minor axis (grey)