A-level Mathematics/CIE/Pure Mathematics 2/Integration

Integration as Reverse Differentiation

Power Rule

The power rule for differentiation states that:

${\dfrac {d}{dx}}x^{n}=nx^{n-1}$

The reverse of this is $\int nx^{n-1}dx=x^{n}+c$ , which can be written as $\int x^{n}dx={\frac {x^{n+1}}{n+1}}+c$

This is the power rule for integration.

Exponentials & Logarithms

Regarding the derivatives of exponentials and logarithms, we know that:

${\dfrac {d}{dx}}e^{x}=e^{x}$
${\dfrac {d}{dx}}\ln x={\frac {1}{x}}$

Reversing these, we get:

$\int e^{x}=e^{x}+c$
$\int {\frac {1}{x}}=\ln |x|$

The natural logarithm takes a modulus input so that it can handle negative numbers.

Note that similar rules apply to any linear expressions that may be composed with these functions:

$\int e^{ax+b}={\frac {1}{a}}e^{ax+b}+c$
$\int {\frac {1}{ax+b}}={\frac {1}{a}}\ln |ax+b|$

Trigonometric Functions

The derivatives of the trigonometric functions are:

${\dfrac {d}{dx}}\sin x=\cos x$
${\dfrac {d}{dx}}\cos x=-\sin x$
${\dfrac {d}{dx}}\tan x=\sec ^{2}x$
${\dfrac {d}{dx}}\tan ^{-1}x={\frac {1}{1+x^{2}}}$

Thus, the corresponding integrals are:

$\int \cos x=\sin x+c$
$\int \sin x=-\cos x+c$
$\int \sec ^{2}x=\tan x+c$
$\int {\frac {1}{1+x^{2}}}=\tan ^{-1}x+c$

As with exponentials and logarithms, this applies to linear expressions that are composed with trigonometric functions:

$\int \cos(ax+b)={\frac {1}{a}}\sin(ax+b)+c$
$\int \sin(ax+b)=-{\frac {1}{a}}\cos(ax+b)+c$
$\int \sec ^{2}(ax+b)={\frac {1}{a}}\tan(ax+b)+c$
$\int {\frac {1}{1+(ax+b)^{2}}}={\frac {1}{a}}\tan ^{-1}(ax+b)+c$

Using Trigonometry when Integrating

Sometimes, it is useful to use trigonometric identities when finding the integral of an expression. e.g. Find the integral

\int 4\cos ^{2}xdx

.

${\begin{aligned}\cos 2x&=2\cos ^{2}x-1\quad {\text{Double Angle Identity}}\\\cos ^{2}x&={\frac {\cos 2x-1}{2}}\\\int 4\cos ^{2}xdx&=\int 4{\frac {\cos 2x-1}{2}}dx\\&=\int \cos 2x-1dx\\&={\frac {1}{2}}\sin 2x-x+c\end{aligned}}$

Trapezium Rule

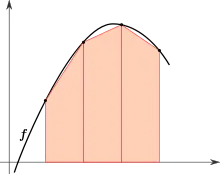
The area under a curve can be approximated using the area of several trapeziums

The trapezium rule states that the area under a curve can be approximated by finding the sum of the areas of trapeziums. The area of a trapezium is given by $A={\frac {B+b}{2}}h$ Where $B$ is the length of the longer side, $b$ is the length of the shorter side, and $h$ is the length of the perpendicular distance between the sides.

In the context of the trapezium rule, each trapezium's perpendicular distance $h$ is a constant $\Delta x$ : the width of each trapezium. The lengths of the sides are given by points on a curve. Thus, for a curve $f(x)$ approximated using trapeziums, each trapezium has an area $A_{i}={\frac {f(x_{i})+f(x_{i+1})}{2}}\Delta x$ .

The area under the curve between the bounds $a$ and $b$ is the sum of the trapeziums' areas: $A=\sum _{x=a}^{b}{\frac {f(x)+f(x+\Delta x)}{2}}\Delta x$ .

Because $\Delta x$ is constant, the expression for the area can be written $A={\frac {f(a)+2f(a+\Delta x)+2f(a+2\Delta x)+\dots +2f(b-\Delta x)+(b)}{2}}\Delta x$ , which can be simplified to $A=\left({\frac {f(a)+f(b)}{2}}+f(a+\Delta x)+f(a+2\Delta x)+\dots +f(b-\Delta x)\right)\Delta x$

Thus, the trapezium rule states:

$\int _{a}^{b}f(x)dx\approx \left({\frac {f(a)+f(b)}{2}}+f(a+\Delta x)+f(a+2\Delta x)+\dots +f(b-\Delta x)\right)\Delta x$

This article is issued from Wikibooks. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.